
Ben Orlin, the modern Maths apologist, brings to us what I’d call his Magnum Opus, the modern Mathematician’s Lament.
Everytime, I read an Orlin book, I always wish, I had teachers like him when I was young, so that I would not have had such crippling math-phobia for so much of my life.
It should actually be called, Maths for the Rest of Us.
It’s great! So great!
My highlights, from the book
A mathematician is hardly a reasonable person. More like a feral philosopher or a logician gone rogue.
It’s a bit peculiar to say that I add 4 and 3 to create 7; 4 and 3 simply are 7, irrespective of my efforts. When I multiply or divide or take a logarithm, the result equals whatever it equals, regardless of my labors. I do not, in a strict sense, change the numbers, but merely discover or reveal them. Operations act not upon the quantities themselves, but only upon our understandings of them.
In my childhood, back when money was made of metal and paper instead of software and lies, I learned that two quarters add up to 50 cents: 25 + 25 = 50. I loved knowing this
… the beauty of mathematical language lies in its unreality. Math lets us escape this world of crumbs and mud for a realm of rigorous abstractions. The purer the logic—that is, the further from physical reality—the deeper the truth. “As far as laws of mathematics refer to reality, they are not certain,” said Einstein, “and as far as they are certain, they do not refer to reality.”
I sometimes envision mathematics as a tower. It leads from the earthy crust of everyday experience (piles of cookies; buckets of water; half-dollar coins) up to the thin atmosphere of abstract concepts (Lie groups, whatever those are). There’s pleasure and power in climbing to the upper floors. But there’s an equal pleasure—and a different kind of power—in descending to the bottom. Down there, you can touch the foundations, poke at the joints where math attaches to the world, and fill your half-gallon bucket with a new kind of insight
Consider 2 + 3. If + is a verb, then who is the subject carrying out the addition? Neither 2 nor 3 performs any action; those nouns just sit there being nouns. You’re the one who adds, but you’re not a part of mathematical speech
Such confusion is not limited to the youth. Adult textbook authors have been known to include gratuitous fighter jets and non sequitur cheetahs, as if the secret to math is picturing something, anything. But the hard part of math isn’t remembering what cats look like. It’s making sense of abstract ideas.
The challenge of algebra is to visualize the invisible
“The point of doing algebra,” writes math teacher Paul Lockhart, “is… to move back and forth between several equivalent representations,depending on the situation at hand and depending on our taste. In this sense, all algebraic manipulation is psychological.”
Old information, new formation
I like this rule because it’s rarely even taught. Mathematicians apply it automatically, the way fluent English speakers always say “a big ugly bath toy” and not “a bath ugly big toy.” In fact, as Mark Forsyth points out in The Elements of Eloquence, English adjectives are typically placed in a certain order: opinion, size, age, shape, color, origin, material, purpose. Hence, “a lovely little old rectangular green French silver whittling knife.
Likewise, in math, numbers are typically multiplied in a certain order: numeral, radical, constant, variable. Hence, we write 3πxy2z, and never (unless we’re trying to provoke someone) zy2πx3
Toward the end of a sixth-grade lesson, a chipper young fellow named Kieran raised his hand. “I don’t really understand anything you’re saying,” he informed me. “But I can still get the right answer.” He beamed a patient smile.
I stifled a sigh. “Which part can I help you with?”
“Oh, I don’t need help,” he said. “It’s just that you were talking about this extra stuff. Like, the ideas behind it. I don’t, you know, do that.”
I blinked. He blinked. A great silence passed between us.
“Is that okay?” he concluded. “I mean, as long as I can get the right answer?”
There it was, out in the open: the subtext of almost every lesson I had taught that year. Day after day, I tried to illuminate the logic behind the symbols. Day after day, my students politely ignored my prattle to focus on the symbols themselves. What made that afternoon stand out was that Kieran broke the fourth wall. He uttered the title of the film we were acting in.
To do math, must you think about the ideas, or can you just focus on the symbols?

As David Hilbert quipped, “Mathematics is a game played according to certain simple rules with meaningless marks on paper.” That’s symbol pushing in a nutshell. Language divorced from meaning
But a few weeks after Kieran’s query, I learned that not all mathematicians share my dim view of symbol pushing. I mentioned to my dad (a mathematician himself) that I had started writing an essay titled ”How to Avoid Thinking in Math Class.” Before I could say any more, he gave the project his stamp of approval. “Great,” he said. “I’ve always said that the point of math education is to help you not to think.”
I was taken aback. No, I explained, the title was ironic. On the question of “Should we think?” I was firmly in favor.
“Oh, yes, thinking is good,” he generously conceded. “But it’s too hard to do all the time.”
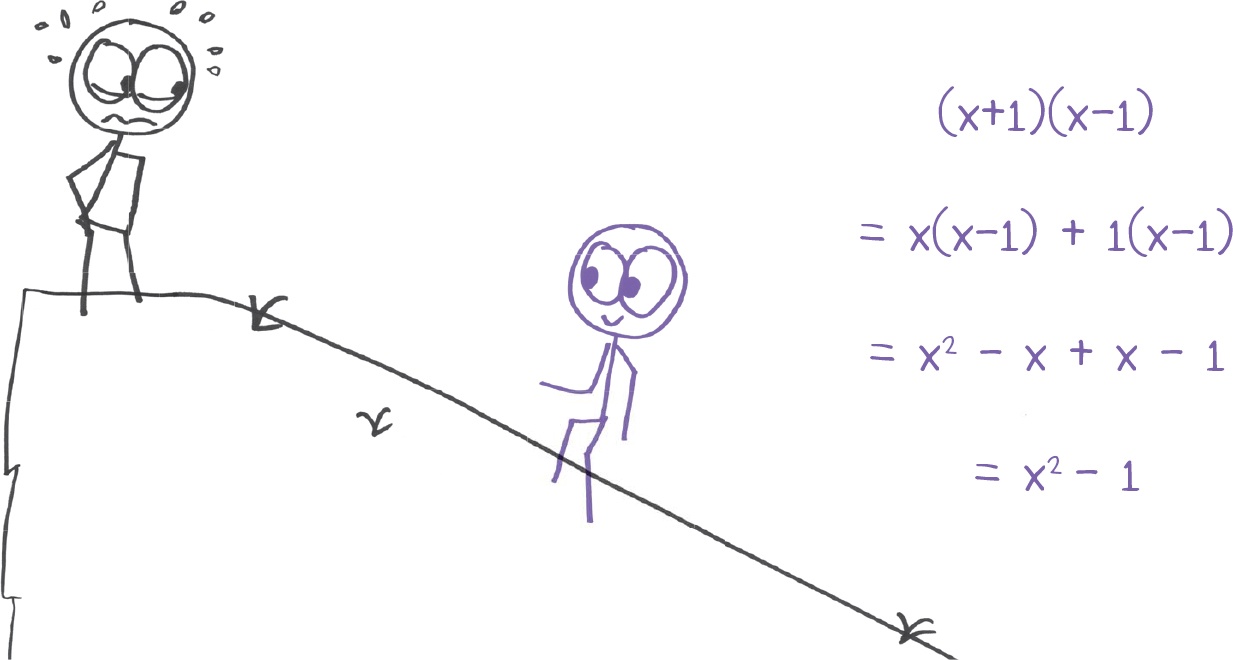
He (and, indeed, Kieran) had a point. For example, it is an algebraic truth that (x + 1)(x − 1) is the same as x2 − 1. This fact boils down to a repeated application of the distributive property; as such, you can explain it entirely in terms of pile rearrangement. But trying to do so is like ascending a sheer cliff face.

Quite a climb! Invigorating as an occasional workout, but unthinkable as a morning commute. This was exactly my dad’s point: Thinking is good. But it’s too hard to do all the time.
“Operations of thought,” wrote the mathematician Alfred North Whitehead, “are like cavalry charges in battle—they are strictly limited in number, they require fresh horses, and must only be made in decisive moments.”
In this case, there is no need to send in the cavalry. The symbol pusher, thinking only about letters and parentheses, reaches the same summit in a few effortless strides
Can you imagine if English worked this way? An object’s name would indicate its physical size, so that a chihuahua (nine letters) would be three times the size of a cow (three letters). A food’s name would encode its recipe, so that a pizza would be a “DoughSauceCheeseBake.” Chemistry would be a tediously safe area of study, because we could run experiments simply by smushing together the names of various chemicals and seeing which ones spell “explosion.”
Symbol pushing boils the laws of logic down to laws of grammar. The language becomes a scale model of reality. We can wrangle ideas simply by wrangling ink.
So who was right, me or Kieran? The answer, of course, is both. To speak mathematics is to slip back and forth between two worlds, to inhabit two distinct frames of mind: the hard joy of thinking and the mindless trance of symbol pushing. Without the ink, the ideas are befuddling; but without the ideas, the ink means nothing. Learn the logic, learn it well, and then turn off your brain and let the symbols on the page dance to the silent music of the mind.
… notations often gain popularity precisely because they lend themselves to simple mechanical rules. You could say we choose the symbols for the express purpose of pushing them around. We can then generate right answers with no insight, no inspiration, no input other than elbow grease. Just turn the crank, and new knowledge pops out
When someone is too focused on details, we say they’re missing the forest for the trees. Mathematicians, if anything, are guilty of the opposite: missing the trees for the forest. Their habit is to inspect not objects themselves, but the objects’ properties. (Not the trees, but the number of them.) Then, having distilled these properties, they look at the properties’ properties. (Not the number, but its evenness or oddness.) And so on: the properties of the properties of the properties of the things. “Matter does not engage their attention,” Henri Poincaré once said of mathematicians. “They are interested in form alone.”
Feedback on this post?
Mail me at feedback at this domain or continue the discourse here.
P.S. Subscribe to my mailing list!
Forward these posts and letters to your friends and get them to subscribe!
P.P.S. Feed my insatiable reading habit.